我太弱了没想到搜索

先说一个结论：

只要时刻t能走到的最远位置可以覆盖x，那么t一定是一个可以到达x的解。

证明(本处只讨论x>0的情景)：

就样例来讲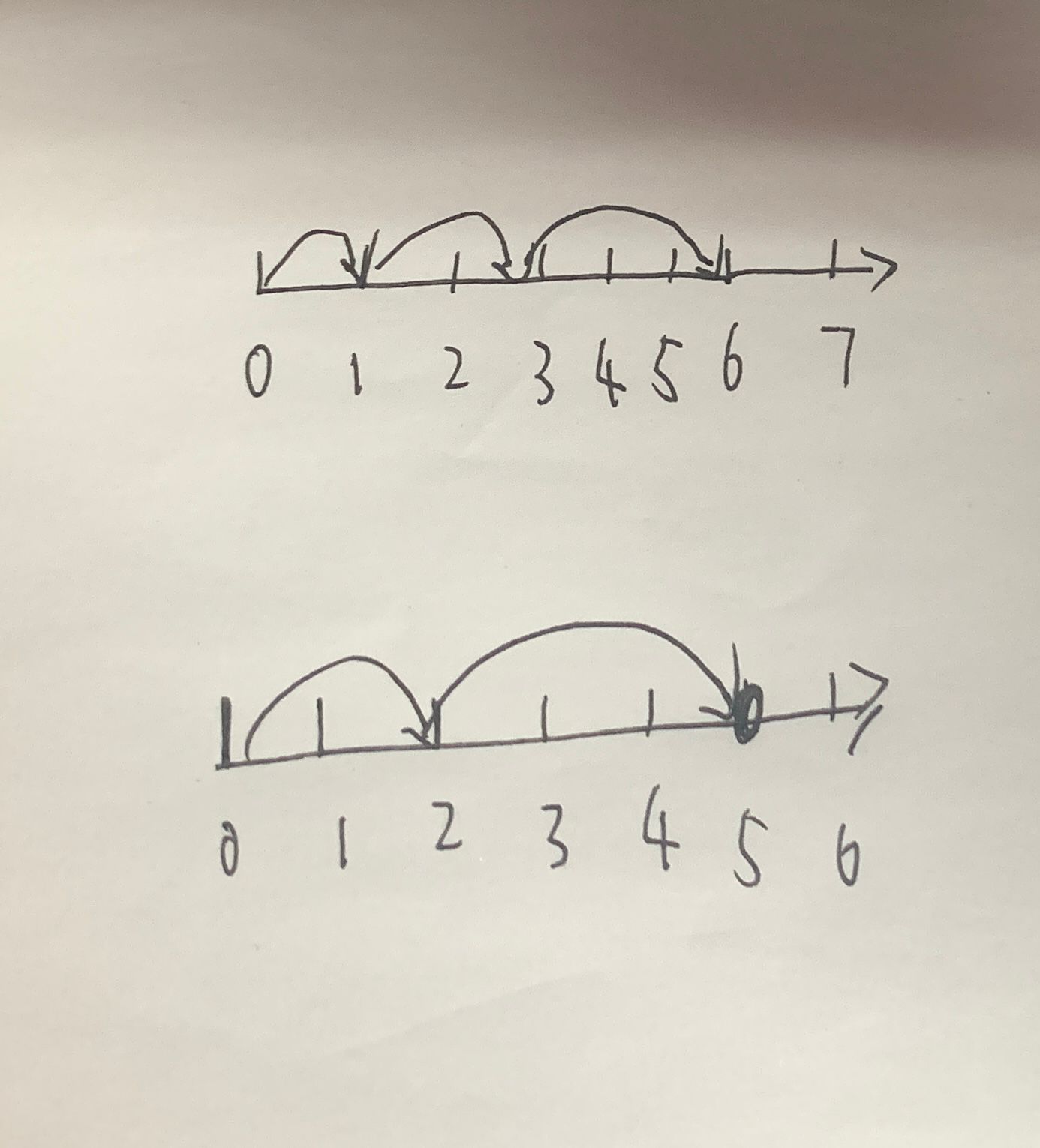： 显然，样例中x=6=1+2+3，所以t=3时可以到达x处。而x=5时候，我们只需要在到达x=6处的步骤中扣除x=1的一步就可以到达，t仍为3，可以证明t=2时只能走到3处，所以t=3便是x=5时的最优解。 我们将这个结论简单推导至一般情况(数学归纳法预警)。 ①t=1时，这个结论显然成立。

②假设t=n时，可以到达最远处为max=n*(n+1)/2，那么我们可以到达0-max中的任意一点。

③t=n+1时，我们的目标点是0-(n+1)*(n+2)/2中的一点。

我们对x分类讨论：

1.x<=n(*n+1)/2时，很显然t=n+1时我们可以到达x处(因为t=n时就可以到达了)

2.n*(n+1)/2<x<=(n+1)(n+2)/2时，我们不妨往前倒推一步(t=n+1时我们必须要移动，否则我们无法到达这么远的x处)，那么问题就变成了在t=n时，走到x-(n+1)处。 而0<x-(n+1)<=max=n(n+1)/2，这正是②中的结论。 综上，可以得出结论：只要时刻t能走到的最远位置可以覆盖x，那么t一定是一个可以到达x的解。

二分过程：

根据这个结论，我们很容易推出：只需要找到一个t，使得t-1可以到达的最远距离<x<=t可以到达的距离，那么t就是最优解。 对于x<0的情形，我们将x取绝对值即可。

AC代码（C/C++）：

#include<stdio.h>
long long x;
bool pd(long long m)
{
	if(m*(m+1)<2*x) return 0;
	return 1;
}
int main()
{
	long long ans=1e10;
	scanf("%lld",&x);
	if(x<0) x*=-1;
	long long l=0,r=x;
	while(l<=r)
	{
		long long mid=(l+r)/2;
		if(pd(mid)) r=mid-1,ans=mid;
		else l=mid+1;
	}
	printf("%lld\n",ans);
	return 0;
}

思路写的很清楚了，就不写注释了。（其实是懒得写）

欢迎大佬指正~