#184. [NOIP1997 普及组] 棋盘问题
[NOIP1997 普及组] 棋盘问题
题目描述
设有一个方格的棋盘
求出该棋盘中包含有多少个正方形、多少个长方形(不包括正方形)。
例如:当 时: 
正方形的个数有个:即边长为的正方形有个;
边长为的正方形有个。
长方形的个数有个:
即
的长方形有个 
的长方形有个: 
的长方形有个: 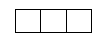
的长方形有个: 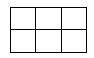
如上例:输入:
输出:
输入格式
输出格式
正方形的个数与长方形的个数
样例 #1
样例输入 #1
2 3
样例输出 #1
8 10
提示
【题目来源】
NOIP 1997 普及组第一题
