#BILFAR. Bill of Fare
Bill of Fare
本题没有可用的提交语言。
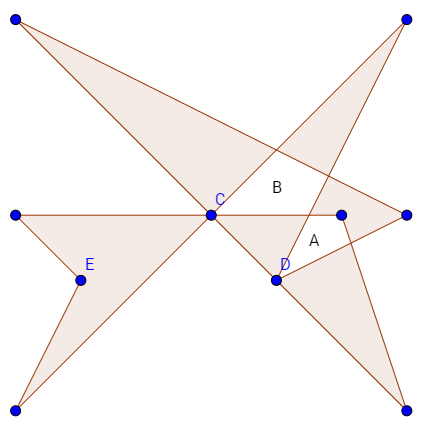
Given a large polygon dining table (not always a simple polygon) with the following properties :
- there is no intersecting area (ex : area A)
- there is no space inside the polygon (ex : area B)
- there is no 3 edges that are concurrent (ex : point C)
- every nodes are not lying on any edge except 2 edges that connect that node with 2 other nodes (ex : point D)
- every nodes forming a convex corner because a table with concave corner is an uncomfortable table (ex : point E)
Example of invalid table :
Given also M dishes with the following rules :
- placed on the table
- not on the edge of the table
- there is no pair of different food that have the same place
You have to answer Q queries :
- each query identified by L and R
- the query is "what is the minimum moves in order to make some dishes (from L-th dish to R-th dish inclusive) placed in same region ?"
- queries are independent
Notes :
- two dishes are considered in same region if and only if from one dish can be slid to another one without crossing any edge
- one move is to slide a dish to another region through an edge
- every dishes should be still on the table, but they may lie on the edge
Explanation :
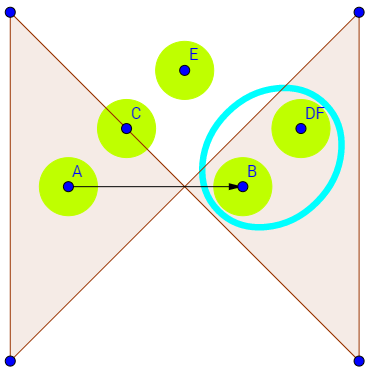
- dish A is valid because it placed on the table
- dish C is invalid because it placed on the edge
- dish E is invalid because it placed outside the table
- sliding from dish A to dish B is considered as one move
- dish B and dish D is considered as one region
- dish F is invalid because it placed exactly on dish D
Input and output format :
- An integer T represent the number of test case, each test case :
- First line contains 3 separated integer N, M, and Q
- Next N lines contain Xi and Yi represent the coordinate of i-th node
- Next M lines contain Pi and Qi represent the coordinate of i-th dish
- Next Q lines contain Li and Ri represent the parameter of i-th query
- You should output Q lines contain the answers of those queries
Constraints :
- 1 <= T <= 10
- 3 <= N <= 1000
- 2 <= M <= 1000
- 1 <= Q <= 1000
- 0 <= Xi, Yi <= 10^9
- 0 < Pi, Qi < 10^9
- 1 <= Li < Ri <= M
Sample input :
1
7 5 3
1 1
1 5
5 1
7 2
7 8
9 5
5 5
6 2
2 3
5 4
8 6
5 3
1 5
2 4
3 5
Sample output :
2
2
1
Explanation of sample :
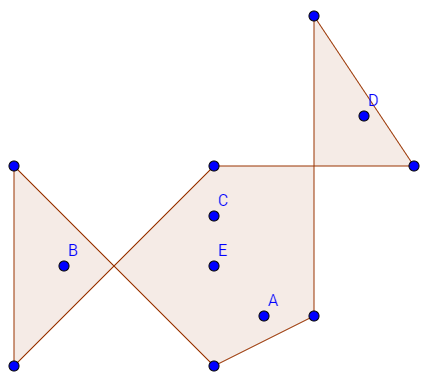
- query 1 : we can slide 2-nd dish and 4-th dish to the middle region
- query 2 : using the same way as query 1
- query 3 : prefer sliding 4-th dish (1 move) rather than sliding 3-rd and 5-th dishes (2 moves)
