[CQOI2017] 老C的方块

题目描述

老 C 是个程序员。

作为一个懒惰的程序员，老 C 经常在电脑上玩方块游戏消磨时间。游戏被限定在一个由小方格排成的 $R$ 行 $C$ 列网格上，如果两个小方格有公共的边，就称它们是相邻的，而且有些相邻的小方格之间的公共边比较特殊。特殊的公共边排列得有很强的规律。首先规定，第 $1$ 行的前两个小方格之间的边是特殊边。然后，特殊边在水平方向上每 $4$ 个小方格为一个周期，在竖直方向上每 $2$ 个小方格为一个周期。所有的奇数列与下一列之间都有特殊边，且所在行的编号从左到右奇偶交替。

下图所示是一个 $R=C=8$ 的网格，蓝色标注的边是特殊边。首先，在第 $1$ 行，第 $1$ 列和第 $2$ 列之间有一条特殊边。因为竖直方向周期为 $2$，所以所有的奇数行，第 $1$ 列和第 $2$ 列之间都有特殊边。因为水平方向周期为 $4$，所以所有奇数行的第 $5$ 列和第 $6$ 列之间也有特殊边，如果网格足够大，所有奇数行的第 $9$ 列和第 $10$ 列、第 $13$ 列和第 $14$ 列之间都有特殊边。因为所有的奇数列和下一列之间都有特殊边，所以第 $3$ 列和第 $4$ 列、第 $7$ 列和第 $8$ 列之间也有特殊边，而所在行的编号从左到右奇偶交替，所以它们的特殊边在偶数行。如果网格的规模更大，我们可以用同样的方法找出所有的特殊边。

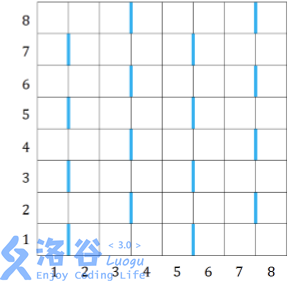
网格的每个小方格刚好可以放入一个小方块，在游戏的一开始，有些小方格已经放上了小方块，另外的小方格没有放。老 C 很讨厌下图所示的图形，如果他发现有一些小方块排列成了它讨厌的形状（特殊边的位置也要如图中所示），就很容易弃疗，即使是经过任意次旋转、翻转后排列成讨厌的形状，老 C 也同样容易弃疗。

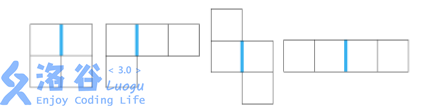
为了防止弃疗，老 C 决定趁自己还没有弃疗，赶紧移除一些格子里小方块，使得剩下的小方块不能构成它讨厌的形状。但是游戏里每移除一个方块都是要花费一些金币的，每个方块需要花费的金币有多有少参差不齐。老 C 当然希望尽可能少的使用游戏里的金币，但是最少要花费多少金币呢？老 C 懒得思考，就把这个问题交给你了。

输入格式

第一行有 $3$ 个正整数 $C,R,n$，表示 $C$ 列 $R$ 行的网格中，有 $n$ 个小方格放了小方块。

接下来 $n$ 行，每行 $3$ 个正整数 $x,y,w$，表示在第 $x$ 列第 $y$ 行的小方格里放了小方块，移除它需要花费 $w$ 个金币。保证不会重复，且都在网格范围内。

输出格式

输出一行，包含一个整数，表示最少花费的金币数量。

样例 #1

样例输入 #1

2 2 4
1 1 5 
1 2 6 
2 1 7 
2 2 8

样例输出 #1

5

样例 #2

样例输入 #2

3 3 7 
1 1 10 
1 2 15 
1 3 10 
2 1 10 
2 2 10 
2 3 10 
3 1 10

样例输出 #2

15

提示

【输入输出样例 2 说明】 如图所示。容易发现，如果不移除第 $1$ 列第 $2$ 行的小方块，则至少要移除两个小方块，才能不包含老 C 讨厌的图形，花费至少 $20$ 个金币；而删除第 $1$ 列第 $2$ 行的小方块后，原有的讨厌图形全都不存在了，只需要花费 $15$ 个金币。

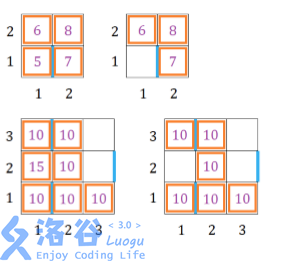
【数据规模与约定】

对于第 $1\sim 2$ 个测试点，$1\le C, R \le 100$，$1\leq n \leq 20$。

对于第 $3\sim 6$ 个测试点，$1 \leq C, R\leq 10^5$，$2000\le n\leq 5000$，数据有梯度。

对于第 $7\sim 10$ 个测试点，$1\leq C, R\leq 10^5$，$30000 \leq n\leq 10^5$，数据有梯度。

对于所有测试点，$1 \leq C, R, n \leq 10^5$，$1 \leq w \leq 10^4$。